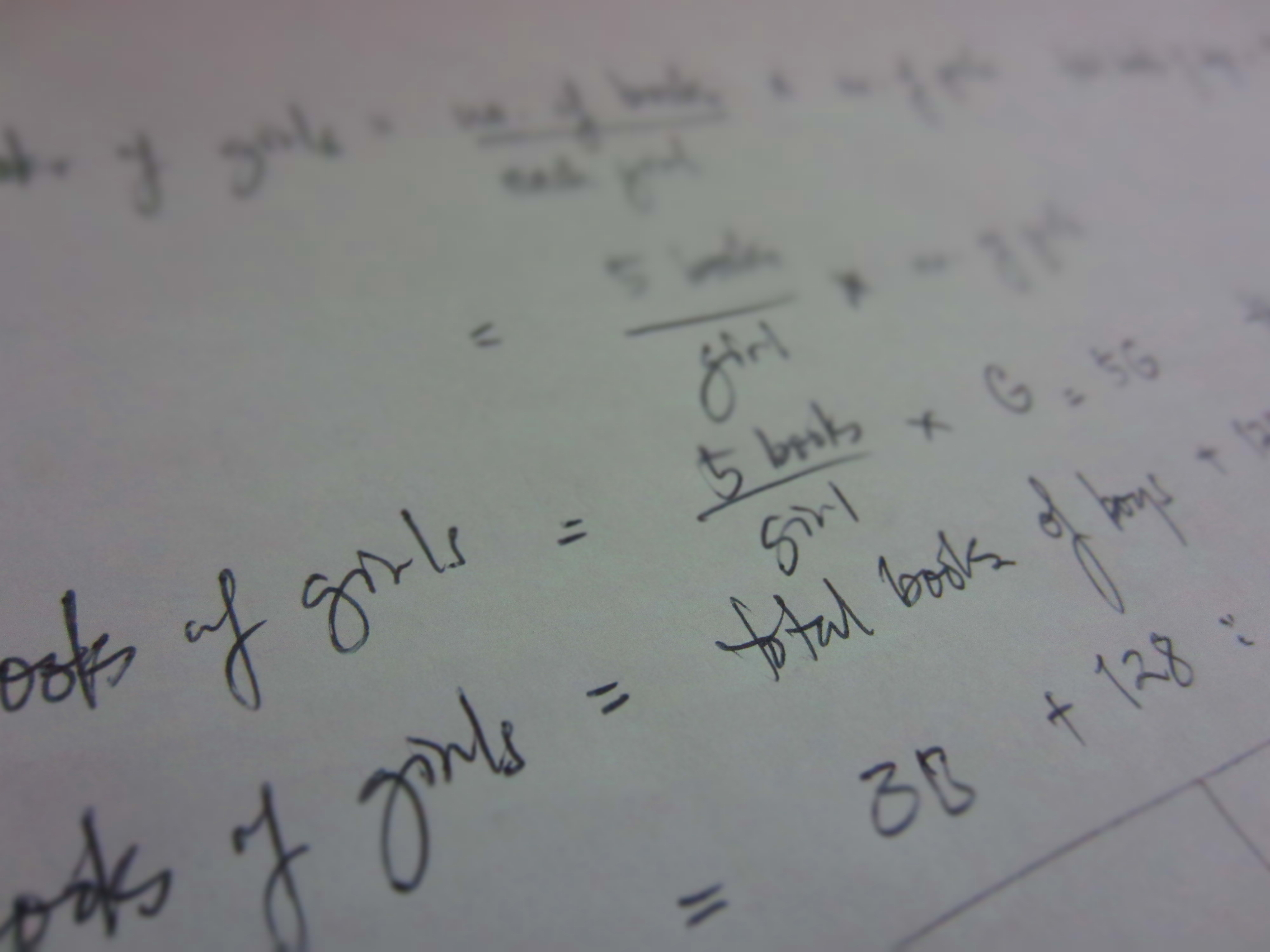Word Problem Set 1

Problem

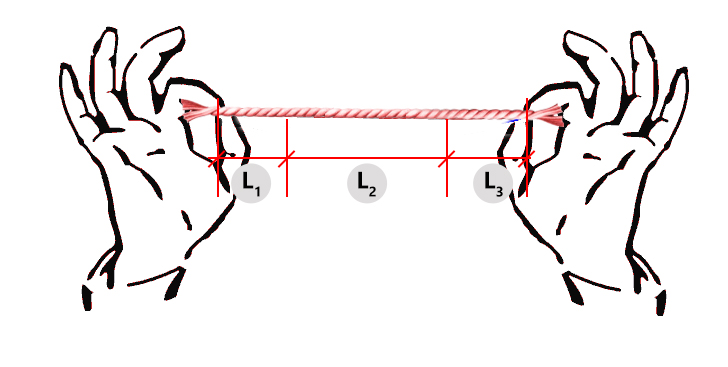
A nylon string is cut into 3 pieces. Two pieces are of the same length. The third piece is twice as long as each of the other two pieces. If the longest piece is 123cm, what is the length of the nylon string?

Given:

L1 & L3 – two pieces of the same length
L2 – longest piece, 123cm
Note that L2 is twice as long as the other two pieces, meaning, L2 = L1 x 2 or L2 = L3 x 2

Asked:

length of the nylon string?

Solution:

Length of the nylon string = L1 + L2 + L3 eq. 1
Note than L1 = L3, so
Length of the nylon string = L1 + L2 + L1 or = L3 + L2 + L3
Length of the longest piece is 123cm, we know that L2 = L1 x 2 or L2 = L3 x 2, hence
L2 = L1 x 2 = 123cm eq. 2
Solving for L1,
2L1 = 123cm
2L1/2 = 123cm/2
L1 = 61.5cm = L3
Therefore, using equation (1):
Length of the nylon string = L1 + L2 + L3 = 61.5cm + 123cm + 61.5cm = 246cm

Problem:

The mass of a basket containing 6 packets of sugar & 3 packets of salt is 2.7kg. If the mass of 12 packets of sugar & 6 packets of salt is 4.74kg, what is the mass of the empty basket?

Given:

Let:
x – mass of basket containing 6 packets of sugar & 3 packets of salt = 2.7kg
y – mass of empty basket
A – mass of 6 packets of sugar & 3 packets of salt
B – mass of 12 packets of sugar & 6 packets of salt = 4.74kg

Asked:

mass of the empty basket (y)

Solution:

x = A + y eq. 1
looking at B, it contains twice as much sugar as A & contains twice as much salt as A, hence,
B = A x 2 = 4.74kg
Solving for A,
2A = 4.74kg
2A/2 = 4.74kg/2
A = 2.37kg
Using eq. 1, substituting values:
x = A + y
2.7kg = 2.37kg + y
2.7kg – 2.37kg = y
y = 0.33kg

Problem:

A rock is 3 times as heavy as a brick. If the difference in their mass is 1.16kg, what is the mass of the brick?

Given:

Let:
r – mass of the rock
b – mass of the brick
r = b x 3 = 3b eq. 1
r – b = 1.16kg eq. 2

Asked:

mass of the brick (b)?

Solution:

Substituting eq. 1 in eq. 2,
r – b = 1.16kg
(3b) – b = 1.16kg
2b = 1.16kg
2b/2 = 1.16kg/2
b = 0.58kg

Problem:

Three boys and five girls sold a total of 1,500 funfair tickets. The boys sold twice as many tickets as the girls. If the two boys together sold 56 tickets more than the third boy, how many tickets did the third boy sell?

Given:

Let:
x – tickets sold by the boys
y – tickets sold by the girls
x + y = 1500 tickets eq. 1
take note, boys sold twice as many tickets as the girls, meaning, x = y x 2 = 2y eq. 2
take note, 2 boys sold 56 tickets more than the third boy, so, 2 boys = 3rd boy + 56 eq. 3

Asked:

tickets sold by the 3rd boy?

Solution:

Substitute eq. 2 in eq. 1:
x + y = 1500 tickets
(2y) + y = 1500
3y = 1500
3y/3 = 1500/3
y = 500 tickets sold by the girls
using eq. 2, x = 2y = 2 (500 tickets) = 1000 tickets sold by the boys
we know the total tickets sold by the boys is,
1st boy + 2nd boy + 3rd boy = 1000 eq. 4
using eq. 3, eq. 4 becomes:
(3rd boy + 56) + 3rd boy = 1000
2(3rd boy) = 1000 – 56
2(3rd boy) = 944
2(3rd boy)/2 = 944/2
3rd boy = 472 tickets bold

Problem:

Mary has three times as many buttons as Susan. Lily has half of what Mary has. Mary and Susan have 96 buttons altogether. How many buttons does Lily have?

Given:

Let:
M – Mary’s buttons
S – Susan’s buttons
L – Lily’s buttons
Take note, Mary has three times as many buttons as Susan, meaning, M = S x 3 = 3S eq. 1
Take note, Lily’s buttons is half of Mary, so, L = ½ x M = M/2 eq. 2
We know that, Mary and Susan have 96 buttons, so, M + S = 96 buttons eq. 3

Asked:

Lily’s buttons (L)?

Solution:

Using eq. 1 in eq. 3, we have:
M + S = 96 buttons
(3S) + S = 96
4S = 96
4S/4 = 96/4
S = 24 buttons
Using eq. 1, Mary’s buttons are:
M = 3S = 3 (24 buttons) = 72 buttons
Using eq. 2, Lily’s buttons are:
L = M/2 = (72 buttons)/2 = 36 buttons