Equipped with our basic equation for distance-time relationship, we know that distance = speed x time. There are a couple of things you need to take note when dealing with distance problems with overtaking scenario and meet with scenario.
By diagram, an overtaking scenario, where two vehicles starts at a distance apart from each other and moving at the same direction, can be graphically shown below:
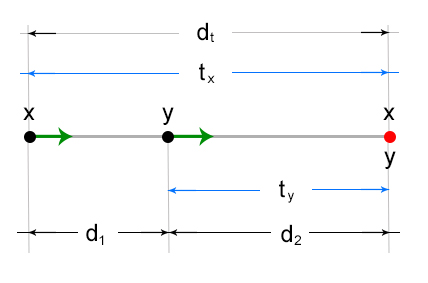
Where:
x – speed of one vehicle
y – speed of the other vehicle
dt – total distance
d1 – initial distance between one vehicle and the other vehicle
d2 – distance between the other vehicle and the overtake point
tx – time travelled by one vehicle
ty – time travelled by the other vehicle
Two key points you need to note on this scenario:
(1) tx = ty
The time travelled by one vehicle (tx) to reach the overtake point (indicated by the red dot in the diagram) is equal to the time travelled by the other vehicle (ty) to reach the overtake point.
(2) d1 + d2 = dt
The total distance travelled is equal to the sum of the initial distance of the two vehicles (d1) and the distance between the other vehicle and the overtake point (d2)
For the meet with scenario, where vehicles travel towards each other and meet at a certain point, can be graphically shown below:
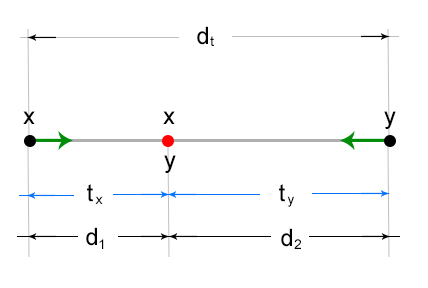
Where:
x – speed of one vehicle
y – speed of the other vehicle
dt – total distance
d1 – distance travelled by one vehicle to the meet point
d2 – distance travelled by the other vehicle to the meet point
tx – time travelled by one vehicle
ty – time travelled by the other vehicle
The same key points as that of the overtake scenario can be used to derived the distance-time relationship for a meet with scenario
(1) tx = ty
the time travelled by one vehicle to the meet point (tx) is equal to the time travelled by the other vehicle to the meet point (ty)
(2) d1 + d2 = dt
the total distance is equal to the sum of the distance travelled by one vehicle to the meet point (indicated by the red dot in the diagram) and the distance travelled by the other vehicle to the meet point.
For application of these key points, click here to sample distance problems.
my biographical info lorem ipsum dolor sit amet

