Problem:
At the beginning of a bicycle ride, Jose and Wally are 30 miles apart. If they leave at the same time and ride in the same direction, Jose overtakes Wally in 6 hours. If they ride toward each other, they pass each other in 1 hour. What are their speeds?
Given:
First scenario, overtaking:
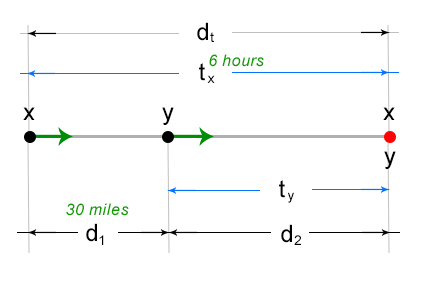
Where:
x – speed of Jose
y – speed of Wally
dt – total distance
d1 – initial distance between Jose’s starting point and Wally’s starting point = 30 miles
d2 – distance between Wally’s starting point and the overtake point (indicated by the red dot)
tx – time travelled by Jose to overtake point = 6 hours
ty – time travelled by Wally at overtake point
Using the two key points in dealing with distance problems (refer to Distance problem: Overtaking & Meet With)
We can establish that tx = ty = 6 hours
And use the second key point to establish our equation:
d1 + d2 = dt
30 miles + ( y (ty) ) = ( x (tx) )
30 miles + ( y (6 hours) ) = ( x (6 hours) )
30 + 6y = 6x
Simplifying:
30/6 + 6y/6 = 6x/6
5 + y = x or x – y = 5 (eq. 1)
Second scenario, meet with:

Where:
x – speed of Jose
y – speed of Wally
dt – total distance apart = 30 miles
d1 – distance travelled by Jose to the meet point (indicated by the red dot)
d2 – distance travelled by Wally to the meet point
tx – time travelled by Jose to the meet point = 1 hour
ty – time travelled by Wally to the meet point
Using the two key points in dealing with distance problems (refer to Distance problem: Overtaking & Meet With)
We then establish that tx = ty = 1 hour
And use the second key point to establish our equation:
d1 + d2 = dt
( x (tx) ) + ( y (ty) ) = 30 miles
( x (1 hour) ) + ( y (1 hour) ) = 30 miles
x + y = 30 (eq. 2)
Using eq. 1, substituting x on eq. 2, we get:
x + y = 30
(5 + y) + y = 30
y + y = 30 – 5
2y = 25
y = 12.5 mph speed of Wally
using eq. 1, we get Jose’s speed:
x = 5 + y
x = 5 + 12.5 mph
x = 17.5 mph speed of Jose
my biographical info lorem ipsum dolor sit amet