Problem:
A worker can finish the painting job in 15 days. Another worker can finish only 75% of that job for the same time. At first, the second worker painted for several days and then the first worker joined him and together they finished the rest of the work in 6 days. How many days each worker worked and what percent of the work has been done by each one of them.
Given:
Worker A finishes a paint job in 15 days
Worker B finishes only 75% of the paint job in 15 days

Asked:
a. Number of days each worker worked?
b. Percent of work done by each worker?
Solution:
LET: W – amount of work done; r – rate of work; t – duration of work
We know that, W = r x t Eq. 1
Plotting the given data, we have:
|
W |
r |
t |
|
| Worker A (WA) |
1 |
15 days |
|
| Worker B (WB) |
75% or 3/4 |
15 days |
Using Eq. 1, we get: r = W / t
Rate of WA (rA) = 1 / 15 = 1/15 per day
Rate of WB (rB) = ¾ / 15 = 1/20 per day
Total work done per day of WA & WB = rA + rB = 1/15 + 1/20 = 7/60 per day
Work done by WA & WB in 6 days = rA+B x number of days = 7/60 x 6 days = 7/10
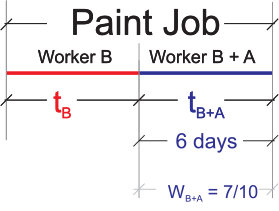
Portion of the paint job that WB worked alone = 1 – WA+B in 6 days = 1 – 7/10 = 3/10
Number of days WB worked alone = WB worked alone / Rate of WB = 3/10 / 1/20 = 6 days
To solved for what is asked on (A), we get :
Number of days Worker A (WA) worked = 6 days Ans.
Number of days Worker B (WB) worked = 6 days + 6 days = 12 days Ans.
To solved for percent of work done by each worker (B):
|
W |
r |
t |
|
| Worker A (WA) |
1/15 per day |
6 days |
|
| Worker B (WB) |
1/20 per day |
12 days |
Work done of WA = rA x tA = 1/15 x 6 days = 2/5 or 40% Ans.
Work done of WB = rB x tB = 1/20 x 12 days = 3/5 or 60% Ans.

