In my continued quest for searching for means and methods of teaching basic mathematical concepts to my grade 3 daughter, I have come up some a way of comparing fractions and arranging them in order.
Before we start, let’s review some basic concepts about fractions. Fractions are numbers representing a part of a whole. A fraction consists of a numerator and a denominator.
3/4 <=> numerator / denominator
|
Where |
Numerator represents the number that describe the parts |
| Denominator represents the number of parts that make up the whole |
Comparing Fractions
Fractions have a wide variety of numerators and denominators depending on a fraction’s size. It is easy to tell for a common fraction such as ½ and 1/3, that ½ is larger than 1/3. But it’s not that easy to tell if 3/8 is larger than 9/16 or is it the other way around.
Quick Tip: If the denominators are the same, the bigger the numerator; the bigger the fraction.
Example:
|
A |
|
B |
|
C |
|
6/7 |
> |
3/7 |
> |
2/7 |
If the numerators are the same, the smaller the denominator; the bigger the fraction.
Example:
|
A |
|
B |
|
C |
|
1/2 |
> |
1/4 |
> |
1/8 |
Comparing Two Fractions
To compare two fractions with different denominators, we use an operation called cross-multiplication. Take for example: Which is larger 3/8 or 9/16?
|
A |
|
B |
|
3/8 |
|
9/16 |
To cross-multiply: we get the product of Numerator A and Denominator B = 3 x 16 = 48; we, then, get the product of Numerator B and Denominator A = 9 x 8 = 72
|
A |
|
B |
|
3/8 |
9/16 |
|
|
48 |
< |
72 |
Hence, 3/8 is less than 9/16 .
Comparing and Arranging Three Fractions
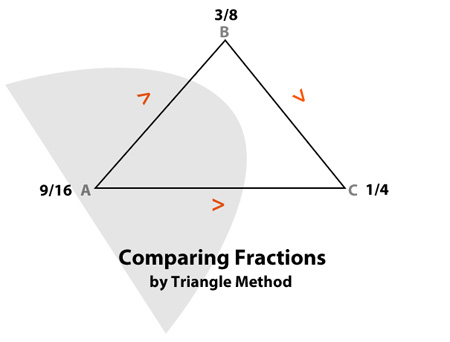
I have devised a way to compare and arrange three (3) fractions, using a triangle method. Take for example: if you are to arrange the following fractions from least to greatest
3/8 , ¼ , 9/16
The triangle method starts by putting these fractions on the vertices of the triangle (in any order, refer diagram below)

Then, you are to compare two fractions based on the legs of the triangle, you can do this by cross-multiplication:
|
Leg AB |
9/16 |
> |
3/8 |
|
Leg AC |
9/16 |
> |
¼ |
|
Leg BC |
3/8 |
> |
1/4 |
Putting in the comparison onto the triangle (refer diagram below)

The fraction with two (or most number of) greater than (>) symbols to it would be the biggest fraction among the three, in this case represented by the gray area which is 9/16. And the fraction with one greater than (>) symbol would be the next bigger fraction, in this case 3/8. Consequently, we are left with ¼ as the least fraction in the group.
So, if you arrange the fraction from least to greatest, the order would be:
¼ , 3/8 , 9/16
Comparing and Arranging Four Fractions
I have come up with a way to compare and arrange four (4) fractions, this time we are going to use the rectangle method. Take for example if you are to arrange the following fractions from greatest to least:
¾ , 7/8 , 5/6 , 2/5
The rectangle method starts by putting these fractions to the vertices of the rectangle (in any order; refer to diagram below)

Then, you compare the fractions based on the sides of the rectangle. Again, you can do this by cross-multiplication:
|
Side AB |
3/4 |
< |
7/8 |
|
Side BC |
7/8 |
> |
5/6 |
|
Side CD |
5/6 |
> |
2/5 |
|
Side AD |
3/4 |
> |
2/5 |
Wait we are not done yet, we are still missing a couple of fractions to be compared, you have to take into account the diagonal BD and diagonal AC (refer to diagram below)

|
Diagonal BD |
7/8 |
> |
2/5 |
|
Diagonal AC |
3/4 |
< |
5/6 |
Put in the comparisons onto the rectangle (refer to diagram below)

The orange area holds the most number of greater than (>) symbols (i.e., 3 greater than symbols), this denotes that 7/8 is the biggest fraction in the group. The green area holds the next most number of greater than symbols (i.e., 2 greater than symbols), in this case ¾ is the next bigger fraction in the group. And 5/6 holds only one greater than symbol making it the next big fraction in the group.
Now, to arrange the fractions from greatest to least would then be:
7/8 , ¾ , 5/6 , 2/5